
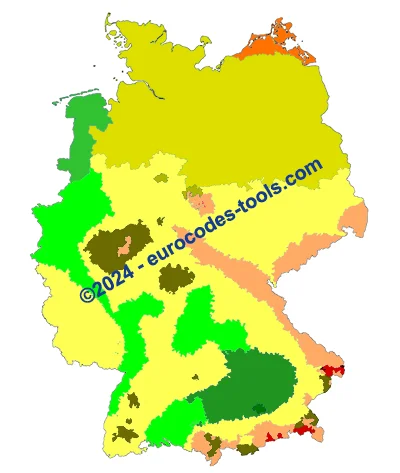
What are the German snow zones according to Eurocode 1 (DIN EN 1991-1-3/NA)?
On the map in the national annex, the German territory is divided into three snow regions marked from 1 to 3. These regions are subdivided into several sub-areas to take account of local particularities leading to increased snow loads and accidental snowfall.
| Zone | 1 | 1* | 1a | 1a*** | 2 | 2* | 2** | 2a | 3 | 3* | >3 | 3a | >3a | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alt ≤300m | Alt >300m | |||||||||||||
| Characteristic value of snow on the ground without altitude sk,0 | 0.65 kN/m² | 0.65 kN/m² | 0.8125 kN/m² | 0.8125 kN/m² | 0.85 kN/m² | 0.85 kN/m² | 0.85 kN/m² | 1.1 kN/m² | 1.0625 kN/m² | 1.1 kN/m² | 1.1 kN/m² | 5.5 kN/m² | 1.375 kN/m² | 5.5 kN/m² |
| Calculation value for exceptional snow load on the ground: 2.3 x sk,0 | – | 1.495 kN/m² | – | – | – | 1.955 kN/m² | – | – | – | – | 2.53 kN/m² | – | – | – |
How do you determine the influence of altitude on snow load on the ground in Germany?
In zones 1 to 3, the characteristic values of the snow loads on the ground must be calculated as a function of the snow load zone and the height of the ground above sea level according to equation (NA.1) to equation (NA.3).
The characteristic values for zones 1a and 2a are obtained by multiplying the values for zones 1 and 2 by 1.25.
Zone 1 (NA.1) :
\[s_k = 0.19 + 0.91 \times \left( \frac{A + 140}{760} \right)^2\]Zone 2 (NA.2) :
\[s_k = 0.25 + 1.91 \times \left( \frac{A + 140}{760} \right)^2\]Zone 3 (NA.3) :
\[s_k = 0.31 + 2.91 \times \left( \frac{A + 140}{760} \right)^2\]For certain locations in snow load zone 3, higher values can be obtained than according to equation (NA.3).
The following areas can be cited as examples:
- Upper Harz
- High altitudes of the Fichtelgebirge
- Bavarian Forest
How do you adjust the snow load on the ground according to the return period in Germany?
\[\displaystyle s_{n} = s_{k} \cdot \left[ \frac{ 1 – V \cdot \frac{\sqrt 6}{\pi} \cdot [\ln(-\ln(1-P_{n})) + 0.57722] } {(1 + 2.5923 \cdot V)} \right]\]- Pn is the annual probability of exceedence :
- dwl is the design working life, in years.
- V is the coefficient of variation of annual maximum snow load with V=0.2 for a recurrence interval less than 50 years and V=0.6 for a recurrence interval greater than 50 years.
- It should not be applied for annual probabilities of exceedence greater than 0,2 (i.e. return period less than approximately 5 years).
Example of results for snow zones in Germany given by Eurocodes Zoning software
The Eurocodes Zoning software allows you to obtain snow loads in Germany free of charge from a GPS point. Try it now!